My Game & Series Prediction Model, Explained | Part 1: Team Data & Game Odds
How SPAM evolved over the last month, and some basic results projection work.
You may have noticed that my game preview cards changed a lot from what I was sharing during the first half of the season.
I’m still bringing you the same key stats and some players to keep an eye on, but the creation of SPAM has opened up 2 new visualization opportunities, a “spider chart” that graph team’s strengths and weaknesses and outcome probabilities.
See this UNH-Maine series preview card as an example:
This isn’t a substitute for watching the games, but we can quickly glean that Maine is a (somewhat heavy) favorite, and their defense, goaltending, and scoring are advantages over UNH. Both teams are battling for pucks and cause problems for offenses well, but Maine is just all-around a better team.
I’m saying a lot of things based on one little chart, so let’s break down how all of this is decided.
🎵 Spider Chart, Spider Chart 🎵
Long-time readers might recognize some of these categories from SPAM, my player value stat for college hockey.
That’s because that’s exactly where they’re from. Now, SPAM has had some structural changes that I will outline in an upcoming blog, but the core idea and goal have remained the same. Assign value to what each player is doing well, or poorly.
I’ve extrapolated this to teams so we can visualize playstyle.
The first step in creating this chart is to add up the total for every player on a team within a category. So, every player’s Goal Scoring, Play Driving, etc.
Each one of these categories is worth something wildly different, so they can’t be charted on the same axis yet. It wouldn’t be helpful to see that the majority of a team’s goals come from their ability to score goals — but it is helpful to see a team’s percentile rank within these categories.
So I calculate this percentile rank, which gives us a number between 0 and 1 for every stat, with .5 as the average. Then on a map, we can get a pretty effective glimpse of teams, their playstyles, and their weaknesses.
Overlapping these charts can also show us where one team might stand out well above another. Here’s BC and BU:
We can see that in the 3 offensive categories, it’s a dead heat. The two teams have so much talent and rank at the top of the nation.
But… BC’s defensive play is a lot better, and their chart extends much further out in these categories. BU still lives in the average/above average part of some of these categories, but they have work to do in order to compete with the Eagles.
Again, this isn’t an exact science. All models are wrong, but some are useful.
Mine is not an exception to this law — but I hope it can help us find the words to describe what our eyes are seeing faster and more accurately than we were before.
It’s also worth mentioning that this chart isn’t predictive but it can help us make predictions. Its cousin, the series outcome pie chart, is focused on making the predictions itself.
Next stop, pies.
This pie chart probably needs less introduction. It’s obvious what it says.
There’s a 45.8% chance Maine sweeps, a 10.4% chance UNH does, and a 43.7% chance they both grab some points.
But how am I figuring this out?
I start with the National Average Goals Per Game. Right now, for 2024-25, this is 2.83.
Then we bring SPAM in. I’ve recalibrated SPAM to always equal goals instead of always equaling points, so we’re able to use it for predictions like this. In theory, because every 1 SPAM is worth 1 Goal Above Average, if we add it to the Average Goals Per Game, we will end up with results close to team’s actual goal output.
We separate this into Offensive SPAM and Defensive SPAM, and then get to work working with this model:
Let’s explain how each step is important.
Calculating Scoring Totals
Step 1: Add a team’s oSPAM to the Average Goals per Game.
This is how many goals you could expect a team to score against a perfectly average defense with a perfectly average goalie.
This is usually pretty close to a team’s actual goals per game, with some margin for error if a team has been overperforming offensively, has played an exceptionally difficult schedule, or just general randomness.
For example: Maine averages 3.4 goals per game, while the number we’ve calculated in Step 1 would be around 3.8.
Maine’s schedule is very difficult though — with mostly above-average defenses and above-average goalies — so if you were to run the model with their specific opponents, the numbers would be much closer to their real-world output.
Step 2: Subtract the opposing team’s dSPAM from this total.
Because dSPAM credits players for preventing goals, it can easily be subtracted from a team’s calculated goal total to get a better idea of how they’d handle a defense of the caliber they’re playing.
Let’s pretend BC, the best dSPAM team in the NCAA right now, is playing against a perfectly average offense with 0 oSPAM, averaging 2.83 goals per game.
Their dSPAM is roughly .97, which when subtracted from 2.83, puts them at 1.86 — .18 above their actual Goals Against per Game — but we haven’t factored in goalies yet.
This .18 gap is made up by BC’s gSPAM multiplier, which I will explain next.
Step 3: Multiply by the necessary goalie’s gSPAM.
gSPAM is brand new and may still have kinks.
But in practice, it’s the ratio between Goals and Expected Goals (which I calculate using some voodoo on InStat — they have a bug on their site that forces me to do some estimation, scaling their xGoals value up to Goals league-wide).
If a goalie gives up 1 Goal for every 1 xGoal they’re expected to, their multiplier would be 1. If a goalie gives up .7 Goals for every 1 xGoal, their multiplier would be .7, and if they give up 1.5, it would be… you guessed it: 1.5.
So Jacob Fowler would bring BC’s Goals Against projection much closer to their actual real-world value, with potential bonuses (or penalties) for opponent play causing game-to-game swings.
This works because the number we calculate in Steps 1 and Steps 2 functions with the understanding that this is how they would perform against an average goalie. It is a multiplier because the a goalie’s production is very workload-dependent.
Goalie A might have 1.5 GSAx and Goalie B might have 1, but if they’re not facing the same workload, then these counting stats don’t work at measuring efficiency
It’s generally accurate enough I’m comfortable using it, but I will definitely be vetting my work as the season(s) continue to go on.
So now we have the above model — let’s so how it does.
Scoring Model Performance
Applying the current parameters to last season’s data and schedule, the average error on teams’ per-game scoring was .19 — so a fifth of a goal.
It’s worth mentioning both of these teams came much closer to their goal projections when the Strength of Schedule bonuses/penalties built into SPAM 2 were turned up—however, I’ll trade better goal total predictions for better winner predictions any time.
Turning this into predictions.
Now that we have a scoring formula, we can apply it to both teams to predict winners. This is pretty simple, right?
If Team A is projected to score 3.3 goals, and Team B is projected to score 2.7 goals, Team A is projected to win. You agree that 3.3 is higher than 2.7, yes?
The problem with using just this projection is the variance from game to game. Are your shooters cold? Are pucks having a hard time getting through? Did the bus take the wrong exit and you missed warm-ups?
Neither of these things are accounted for in the goal projections, so we turn to Pythagorean Wins to figure out the probabilities at play here.
In one sentence: Pythagorean wins take a team’s scoring outputs for and against, and figure out what win percentage this team can expect to have.
The formula is as follows:
The Power of 2 is generally the best practice for Pythagorean wins, and I ran a test to confirm this was the best value for our data as well.
I apply this on a game-by-game basis to get our game and series odds.
So if Team A is projected for 3.3 goals and Team B is projected for 2.7, I plug those numbers into the formula for Team A, and get my probabilities for each team.
Then if I recalculate the numbers for the 2nd game of the series if one of the teams platoons their goalies, and multiply together the different outcomes to get our final series projections. It’s all very simple math that an idiot can do (see: this blog).
We encounter trouble with predicting ties, but this is also something you’ll find that KRACH and GRANT don’t do. It could probably be figured out with different types of modeling, but I’m still learning and won’t pretend I know how to do that yet.
Are these predictions accurate?
Yes!
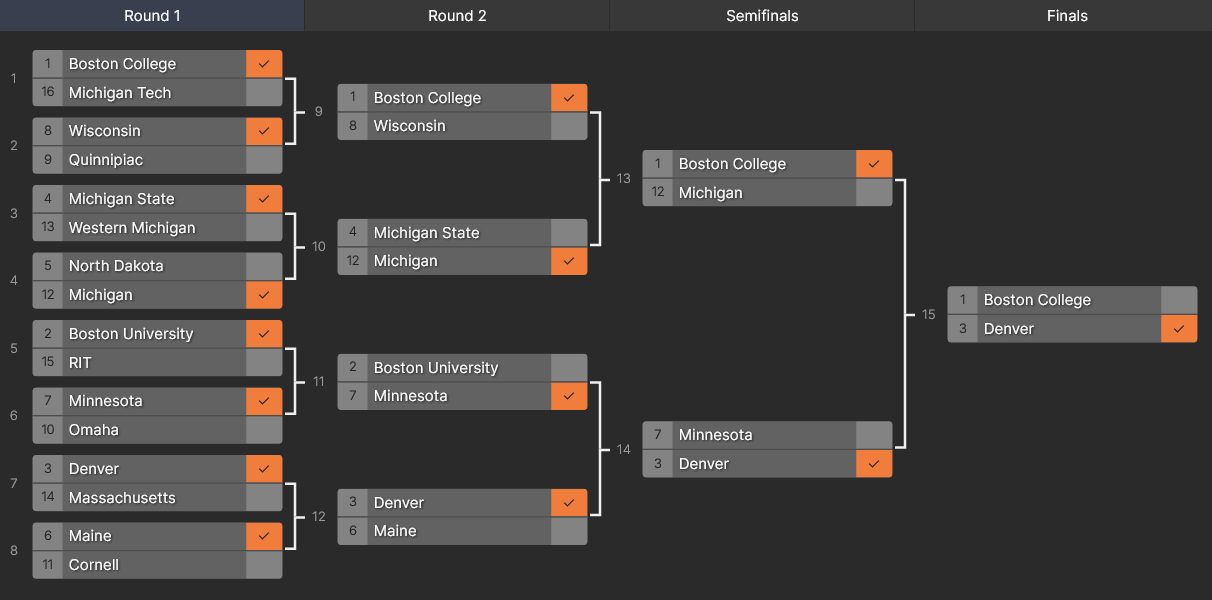
Backtesting the data with 2023-24, the model predicted 68.7% of winners correctly and would have put up a clinic in the NCAA tournament prediction contest I ran.
Starting with the highlights — the model correctly predicted Michigan’s 2 upsets to win their regional and Denver’s title game stunner against Boston College. Vegas had BC as a 73% favorite in this game!
Had someone submitted this bracket, they would have only missed on Quinnipiac-Wisconsin and Cornell-Maine (separated by less than 0.5%) in the first round, and the BU-Minnesota (separated by less than 1%) regional final.
In 2022-23, the results were just barely less accurate, with a 65.3% hit rate. It still would have had 3 of the 4 Frozen Four teams correct (again, sorry BU), but the Cornell-Denver upset in Manchester throws a wrench into the model’s DU Frozen Four trip.
In this digital world, Rand Pecknold’s Disney ending doesn’t happen, as Michigan just barely ekes out the win on Thursday night, but fails to the victors against Minnesota in the final on Saturday.
Looking ahead and room for improvement.
It’s not perfect, but for now, it’s a perfectly viable hockey prediction model.
It’s correct roughly 2/3 of the time, which is slightly above MoneyPuck’s NHL hit rate (≈ 3/5) and a little less than KenPom’s NCAA Men’s Basketball model (≈ 3/4).
Both of these make sense because the NHL is the parity league in pro sports, and NCAA Hoops tend to swing towards gaudy win percentages for favorites.
Focusing on improving my model though:
Offensive play is valued very highly, which makes sense at a fundamental level, but I’d be interested in finding a way to raise the stock of teams that play low-event hockey at title contender rates.
I’d be interested in honing the goaltending multipliers as well. Should defenses and goalies both have be multiplier? I’m thinking about how this would be implemented, and it makes sense.
The model also doesn’t take into account injuries, which are very real in this sport. Theoretically, lineups could be set on a per-game basis in the file I run the Pythagorean Wins formula and create the game cards in, so it might be worth considering — but for now, I’m not focused on it.
With all of this in mind, I’m happy with what I have and will continue to work on it.
I’ll have a more complete explanation of the changes to SPAM within the next two weeks — I’m lucky enough to be attending the Beanpot Final and Four Nations Faceoff this month, so time to write is going to be rare… but I’ll find a way.
See you for the Week #20 Preview on Thursday, and this upcoming weekend for a write-up of “SPAM 2” for player and team evaluation.









